Complex Transformations – The Complex Logarithmic Function

Posted on September 21, 2011 by Anuj Varma

The real logarithmic function has two interesting properties:

The Flattening property: 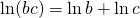$\ln(bc) = \ln b + \ln c$ – a product is flattened into a sum
The Linearizing property: 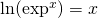$\ln (\exp^x) = x$ –> Linearized an exponential (growth) function

These properties show the general ‘tone it down’ nature of the logarithmic function. It’s nature is to curtail/tone down growth.

How do these properties carry over to the complex world? Let us look at the complex transformation $w = \ln z$

The Flattening property for the Complex Logarithm

FAILS – because of the multivaluedness of the complex logarithm e.g.

$\log(-\iota 1 ) \neq \log(1) + \log(-\iota)$

$RHS = \log(1) + \log(-\iota) = \iota \pi + \iota \frac{\pi}{2} = 3\iota \frac{\pi}{2}$

$LHS = \log(-\iota) = -\iota \frac{\pi}{2}$

The LHS and RHS differ by $2 \pi$

The Linearizing property for the Complex Logarithm

FAILS – because of the multivaluedness of the complex logarithm (it only works inside the principal strip)

$\ln(\exp^z) = z$

The principal strip is the strip in the w plane defined by : $w = u + \iota v$ such that $-\pi < v \leq \pi$

So – both the linearizing and the flattening property only hold true in a limited manner for the complex logarithm.

Circles Transformed to Straight Lines

Some other interesting properties that complex logarithms exhibit include:

A circle with center at the origin (in the z plane) is mapped to parallel lines in the w plane.

z-plane	w-plane

(1) $\begin{equation*} w = u + \iota v = \ln z = \ln (r \exp^(\iota \theta) ) = \ln r + \iota \theta \end{equation*}$

(2) $\begin{equation*} u = \ln r \text{Equation of a straight line (x = constant; i.e. x = vertical lines)} \end{equation*}$

(3) $\begin{equation*} v = \theta \text{Equation of a straight line (y = constant; i.e. y = horizontal lines). This means that rays emitted from the origin will be mapped to horizontal lines in the w-plane.}  \end{equation*}$

Circles with radius r are mapped to u = ln r. Rays emitted from the center are mapped to horizontal lines. See the figure for lines corresponding to circles of radius r=1/2, r=1, r=3/2

Applications

The above property is useful in solving physics/engineering problems where disks are involved (disk shaped fields etc. can be transformed to vertical lines using the above property of the complex logarithm).

Summary

The complex logarithmic function shows behavior that is in start contrast to the real logarithmic function. Mappings using this function provide a way to turn circles into straight lines – which lends itself to solving certain engineering problems.

The Flattening property for the Complex Logarithm

The Linearizing property for the Complex Logarithm

Circles Transformed to Straight Lines

Applications

Summary

Leave a Reply Cancel reply