N Points on a unit sphere
Problem Statement
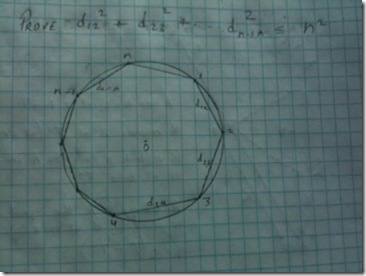
Consider n points lying on the Unit Sphere (the image shows a unit circle instead of a sphere). Show that the sum of the squares of the lengths of all segments determined by the n points is less than 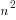 .
.
Potential Stumbling Block
n is the NUMBER of points. It seems a bit counter-intuitive to think of the lengths of the segments related to the number of points on the unit sphere. Yet – that is exactly what this problem is asking us to prove.
Baby Steps
Perhaps the first realization should be that the sum of the squares of lengths is sought. So – we should probably think in terms of the vectors representing the segments – so that we can take an inner product (which will be a squared length).
- Let O be the origin
- Let
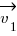 be the vector connecting O and a point 1 (one of the n points). Then the vector
be the vector connecting O and a point 1 (one of the n points). Then the vector 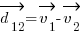 (see the image below). A given segment’s length is just the difference in length of the two vectors radiating from the origin:
(see the image below). A given segment’s length is just the difference in length of the two vectors radiating from the origin: 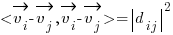
Adolescent Steps
Now that we have a way to describe the length of an individual segment, let us denote by S the sum of all such segments:
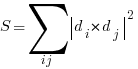
- Now, the trick is to realize that 2 times the Sum :
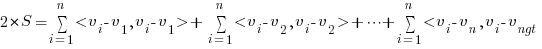
- Once we have the above expression for 2S, the rest is just algebra:

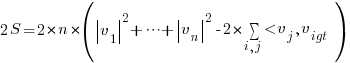

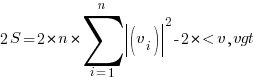

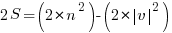
Final Step
The above expression shows that 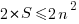 . Hence,
. Hence,
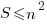 i.e. the sum of the squares of all segments is less than
i.e. the sum of the squares of all segments is less than 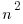 .
.
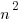 .
.
Leave a Reply